In 1852 a South African mathematician asked a seemingly simple question that triggered endless dispute, left a trail of overturned publications in its wake and culminated in a resolution that has stretched the very tenets of math.
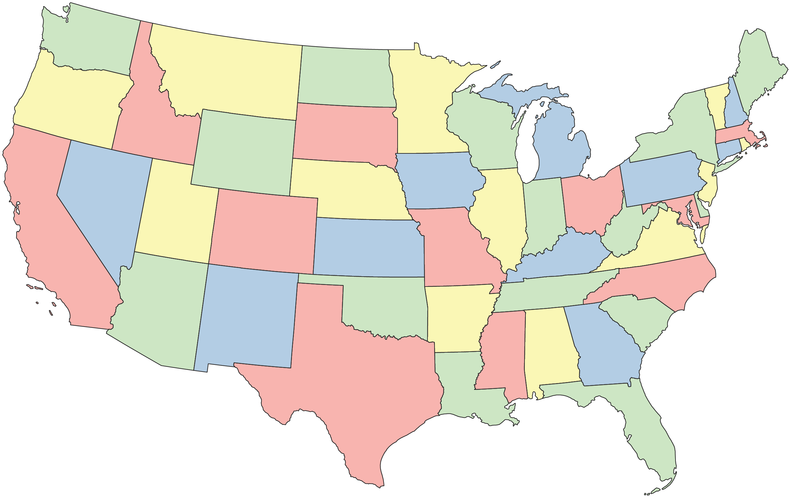
The color conundrum that stirred up so much trouble: What is the fewest number of colors needed to color a map so that no neighboring states or other designated areas have the same hue? Here’s how it works. Check out the map of the contiguous U.S. below.
It looks a little bare-bones. To make maps more vivid and clearly highlight their borders, cartographers tend to color in the regions like so:
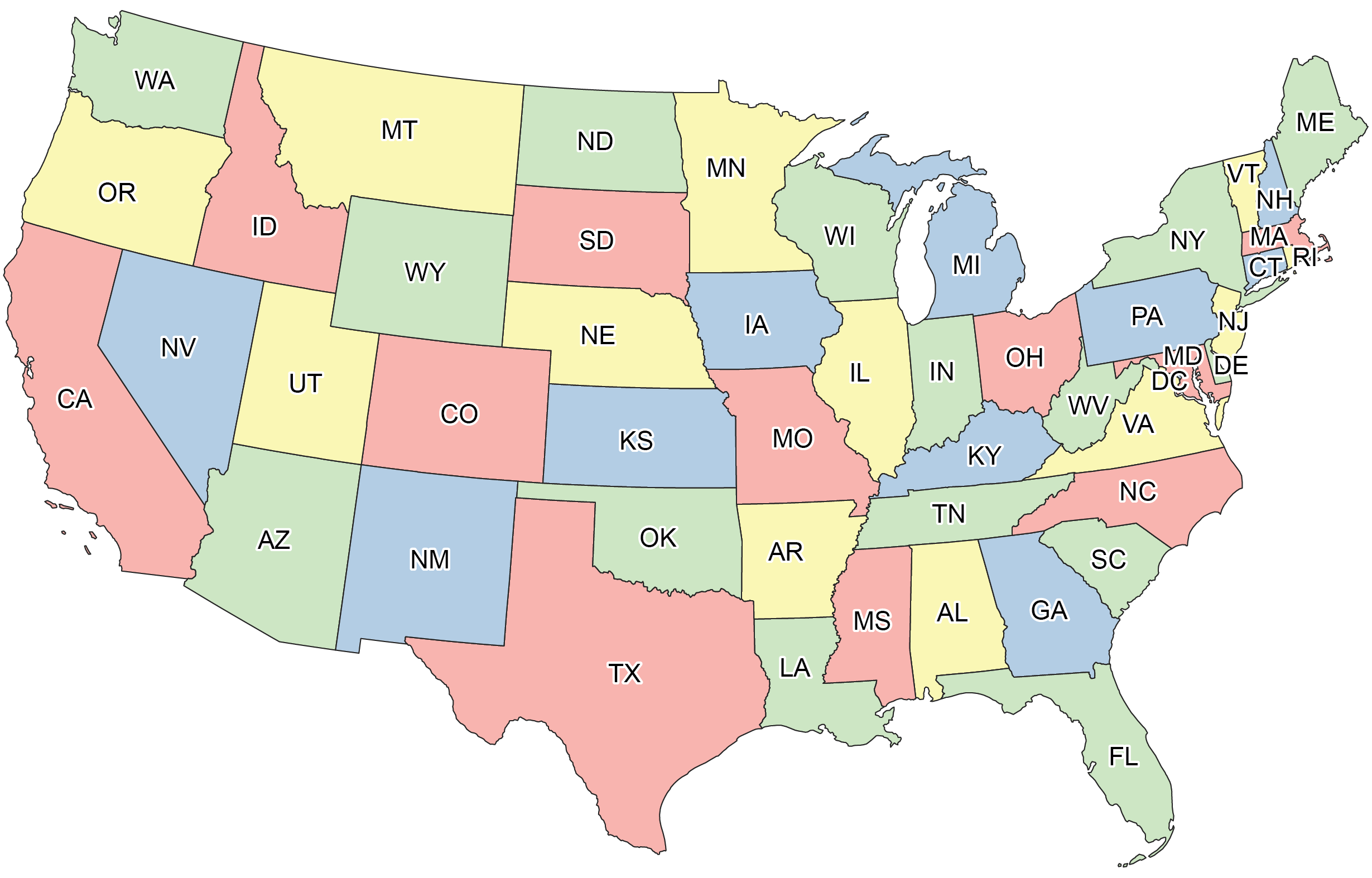
Naturally, we don’t want neighboring states to have the same color, because that would make the boundaries more confusing. Under this constraint, we used four colors to fill in the map above. Could we have done it with only three? Might other maps require five or six?
The map doesn’t need to correspond to real geography—any partitioning of a flat surface into distinct regions qualifies. The question is, given any such map, what is the minimum number of colors required to fill in each region so that no two adjacent regions have the same color? Some ground rules: each region must be contiguous, so technically Michigan violates the setup because Lake Michigan severs the state into two disconnected parts. For two regions to count as adjacent, they must share some contiguous border; touching at a single point (or discrete set of points) doesn’t qualify. For example, Utah and New Mexico famously only touch at a corner and so do not count as neighbors for our purposes.
With the rules established, here are some questions with surprising answers. Suppose I printed out a large poster with a complicated map containing a few thousand regions. How long would it take you to determine whether the map could be colored with two colors? Three colors? Four colors? You don’t necessarily need to…
Read the full article here