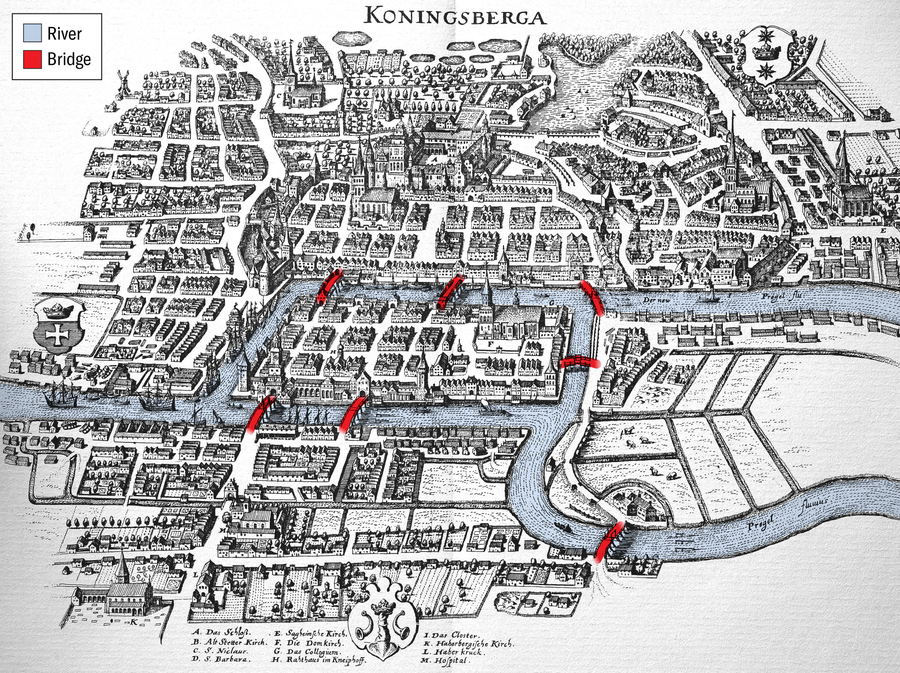
During the 18th century the denizens of the Prussian city of Königsberg wrestled with a puzzle: How could they find a walking path through the city that crossed each of its storied seven bridges exactly once?
The bridges spanned a river containing two large islands. No matter how much they strategized their routes, they couldn’t avoid repeating a bridge.
The problem stymied local thinkers, who eventually wrote a letter to famed mathematician Leonhard Euler (pronounced “oiler”) begging him to lay their curiosity to rest. Euler responded dismissively, claiming the problem had “little relationship to mathematics.” In a way, he was right, because the relevant math hadn’t been invented yet. Despite his initial demurral, Euler did end up solving the puzzle of the seven bridges of Königsberg, unaware that in the process he had birthed two new branches of math.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The Prussian city of Königsberg, now Kaliningrad, Russia, in the Middle Ages. The 18th-century city map is a digitally enhanced reproduction that was modified to highlight river and bridges.
Alamy Stock Photo (map); Amanda Montañez (highlighting)
Say you were a resident of Königsberg. Looking at the map above could you design a path that traverses every bridge once? You’ll have to think like a mathematician. The first hurdle in wrangling any math problem is to strip away extraneous information until only the essential elements remain, a process called abstraction. Many features of the map don’t affect the question at hand. The lengths of the bridges, the sizes of the landmasses, even the geographical orientation of the land and bridges can all be discarded. All that matters is which pieces of land connect to which other ones and…
Read the full article here